Does Size Matter?
Let's talk about school size, shall we?
Ask anyone and they'll tell you that the bigger a school is, the better they are at basketball. There's some sound logic in this. The more kids you've got, the more basketball players you've got to choose from when putting together your team. Simple enough, right?
But, still the dream exists of that small school that can beat the big school, the 16 seed that knocks off the 1. There's a reason Hoosiers is the greatest sports movie ever made. People want to see the big upsets. They want Hickory to win the whole thing. They'll sit through blowouts in the hope of seeing a miracle. It's kind of one of the essential truths of sports.
But here in Maine, we don't really allow for that. Even though our enrollment sizes are much more compressed than elsewhere.
Take Indiana, for example. They have 4 classes (1A through 4A), with enrollment like this:
1A: 62-314 students
2A: 200-529 students
3A: 411-1094 students
4A: 738-4830 students
Let's look at 3A. That's basically the range of Mountain Valley (418) to Oxford Hills (1074) in the same class. Basically they would lump our 5 classes into 3 classes (with quite a bit of overlap) and then have another one on top of that. We have 6 Class A schools that would be big enough to play in a class with a school that's the size of Portland, South Portland, Deering, Oxford Hills, and Edward Little combined. Imagine Brunswick having to play an all-star team of Portland, South Portland, Deering, Oxford Hills, and Edward Little. You can't, can you?
Last season, the 4A championship featured the 31st largest school beating the 50th largest. The 3A champion 2 years ago has 700 students, basically what Hampden has. They went 54-2 over two seasons. The 1A champion has 74. You know, 3 more than Valley.
In Indiana, MDI and Portland would be in the same class. Hell, Portland and Winthrop could be in the same class. But in Maine, we put Portland in AA and MDI in B (and Winthrop in C), because MDI couldn't possibly compete with Portland.
No one questions the logic in this.
Yet, the smallest A school is undefeated. The second smallest B school is 12-3. Even Portland, the #1 team in our Media Poll, is barely big enough for AA.
Why are we so quick to assume that class size equates to talent? Luckily, we have cross-over games that can tell us quite a bit about how a small school would do against a big school. Going into yesterday's games, it looked like this:
W-L of Bigger School
AA v A: 19-14 (57%)
A v B: 29-16 (64%)
B v C: 54-33 (62%)
C v D: 62-48 (56%)
That's a decent win rate, but it isn't wonderful. If my computer model picked games at that right, I wouldn't show it to anyone. Let's break it down a little further:
AA vs A (non-playoff): 8-2
AA vs A (all playoff): 11-12
AA schools are 8-2 against Class A schools that probably aren't going to the tournament. As they should be. But they're 11-12 against everyone else. That's not great. It's pretty mediocre. They're 3-7 against the Top 5 in A North & South, according to the Heal Points. Westbrook is 3-1 against AA. That's bad.
Or, to put it more bluntly: If Class AA was in Class A, they'd be looking at a play-in game.
But let's look at it differently. Let's run those games through the model, which makes adjustments for a variety of factors, including what class a school plays in. Here's those same games, broken down by who the model thinks should win, regardless of what class they're in:
W-L of Higher Ranked Teams in Cross-Class Games
AA v A: 27-6 (82%)
A v B: 39-6 (87%)
B v C: 66-21 (76%)
C v D: 89-21 (81%)
Basically, the higher ranked teams beat the lower ranked teams, no matter what class they're in.
But that's a pretty small sample size and maybe it doesn't represent schools that don't play cross-class games? With that in mind, I pulled the enrollment numbers for each school and compared them to the Heal Points for an entire class. It's a little time-intensive, so I started with Class A, which looked largely representative of the other classes.
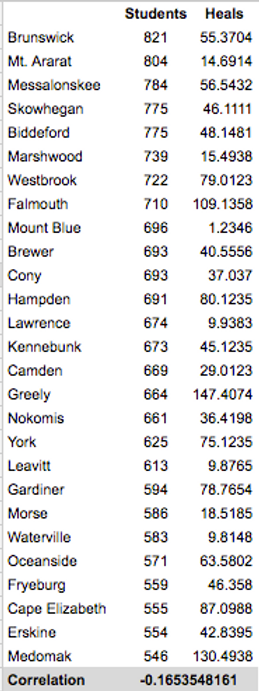
A correlation of -0.17 basically means that not only is there zero correlation between enrollment and results (i.e. results don't improve with more kids), but there's a (very) slightly negative correlation. I didn't bother doing the rest. In other words:
School size has zero impact on a team's ability to win. Zero.
The basketball reason for this is pretty simple: in high school basketball, 3 good players can win you a lot of games. One great player can win you a ton of games. You don't need the numbers you need in football. And as I like to tell people, the next Jimmy Chitwood could just as easily be born on Vinalhaven.
You want another test for this? Just look at the standings for the boys and girls.
A good basketball program can easily overcome some (but not all) of the disadvantages of size. So can a good coach. But both, paired with a talented group of kids? That can be everything. It's just easier in AA than it would be in D. You get more chances at it.
Which brings me to my larger point: don't automatically assume a school in AA would destroy a school in C. The numbers aren't there. If you want to argue that a Class AA team would win because it's a bad matchup for a Class C school, ok. But in Indiana, schools with 1,500 students routinely beat schools with over 4,000. That's a difference of 2,500. Portland has 641 more students than Winthrop. That's nearly the difference between Portland and Thornton Academy. It doesn't seem to bother them.
If you want to truly know if a Class C school could beat a AA school (and they totally could), there's only 1 way to know for sure: put them on the court with something to play for.

Comments ()